Those who really know me, know one of my passions in life is exploring and theorizing the possibilities of the significantly-beyond-now. Also known as: the future.
I like to consider myself an avid science fiction fan, modest creative-thinker, and to a mediocre degree, author. For this, I find myself highly qualified.
1. I have a degree in Astronomy.
2. I've spent more time in an observatory than I'd like to admit. (Sometimes actually observing...)
3. I've had night-long discussions with fellow astronomers and egg-heads about theoretical physics...
4. I've seen Star-Wars.
Okay, so what about the oranges?
Well I was cooking my dinner tonight, which consisted of a delicately simmered duet of chicken breasts, smothered in a special blend of soft spices, with some lemon, and a bit of orange. While I was peeling said orange, I was reminded of a lecture I attended about a year ago from a leading astronomer who was studying the shape of black holes.
Curiously, black holes aren't always round. Didn't know that? Keep reading, it gets better...
Turns out there are basically two kinds of black holes (that we know of). The kind that spin, and the kind that don't.
As we know from physics, things that spin tend to get flatter. The Earth is a good example, as is the Sun. So is clay on a potter's wheel if the potter walks off to discuss quantum singularities while the motor's still running...which I hear they do a lot...
Anywho, back to the black holes.
A scientist by the name of Karl Schwarzschild spent some time in 1916 playing around with Einstein's field theory equations and came up with a little thing we astronomers like to call the "Schwarzschild Radius." Basically this is the distance from a massive object at which any mass cannot avoid collapsing to a gravitational singularity. In plain-speak, it's the point at which an object's own atomic forces cannot keep the object from shrinking any smaller. Our own Sun is kept from imploding under its massive gravitational force, by the outward force of the fusion reactions inside it. If it weren't for this outward force, the Sun would keep crushing itself smaller and smaller until it became what we astronomers call a "singularity" which is a fancy name for a zero-volume thingy where all the mass went.
So if you had a really massive object...like, hmm...a black hole...the forces causing mass to collapse in would be so great that there would be a point at which any mass would collapse towards that massive object. This is the Schwarzschild radius.
Still with me? Great!
Okay, so we know black holes suck things into them. That's not correct phrasing, but pthtptpt!
We call black holes that don't spin "Schwarzschild Black Holes," because they need a name and "Schwarzschild" is cool-sounding. :)
Actually, they're called that because there is a clearly defined point or radius at which matter traveling towards the gravitational center of the black hole both cannot escape, and cannot avoid being crushed into the singularity, despite its own atoms protests. Schwarzschild black holes are great to work with, because they are nice and docile and don't do anything fancy that messes with normal equations...like spin.
Unfortunately, it is theorized that most black holes spin. We believe this because black holes are formed from massive objects, called stars, which were once spinning. It's very hard to stop an object as massive as a star from spinning. You either need another equal-mass star...or a lot of tiny objects...like...trillions upon trillions upon trillions upon trillions of them... That's another physics issue to talk about later, though.
Okay, so we call rotating (spinning) black holes "Kerr Black Holes" after another famous (well, not so famous) scientist, named Roy Kerr, a New Zealander who got this particular bit of fame in 1963.
Roy Kerr is famous for developing some math equations, known as "Kerr metric," that described the geometry of spacetime around a massive object, such as a black hole. The math will kill brain cells and drive you insane, but from the fingerpaint perspective it's cool stuff.
Get to the point.
Okay, so the point I'm getting at while peeling my orange is that black holes actually deform as they spin. Why is this significant? Well, we all consider black holes to be...well...holes... In a Schwarzschild black hole, that's a pretty good lay-speak way of explaining things. However, in a Kerr black hole, you have a ring. (Trust me, this is a lot more fun when beer is involved...)
Okay, so why a ring now? Well, a funny thing happens when a black hole spins. You see, there's this thing call the "event horizon" which is a catchy term for a spherical boundary at which matter and light can no longer escape the gravitational pull of the black hole singularity. This has been popularized over the years by countless science fiction films, and is probably the part about black holes people know best, and actually get correct. Again, there IS NO HOLE IN A BLACK HOLE!!!
When a black hole spins, it develops two event horizons, actually. One is known as the event horizon, and the other is something we call the "Stationary Limit." The stationary limit is another spherical boundary that defines where an object can not only avoid dropping into the black hole, but remain stationary. You have to be going at the speed of light to make this happen, but we won't split hairs. The key here is that in a Schwarzschild black hole the two horizons are one in the same, while in a Kerr black hole they diverge. The Stationary Limit actually bows out at the equatorial point of the spinning black hole, while at the same time touching the poles of the event horizon sphere. It kinda looks like this, if you could draw it:
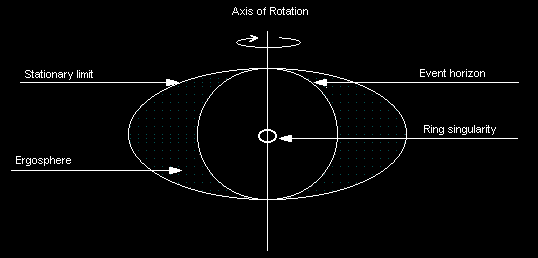
Wait, Shoobie...What happened to the ring?
Turns out that a spinning black hole's singularity becomes stretched around it's angular axis (the point in the center) and forms into a ring singularity. This is where the hard-wood physics in most people's brains breaks down and they either get really violent, or start drooling. Just don't send me any hate mail, okay?
What does this have to do with shape, Shoobie? This was supposed to be about the shape of the black hole!
Okay, so you may not be able to see an event horizon, or a stationary limit...but you CAN see the effects of it. According to the laws of particle physics, both horizons will have a photon sphere. A photon sphere is a spherical plane where photons gather, either because they're orbiting, stationary, or just entering the black hole. To tick your brain, photons that enter the black hole traveling WITH its spin (that is, traveling in the same direction as all the stuff the black hole is dragging around it), the photon will nest itself in the inner photon sphere, at the event horizon. If it's going the other way, it will circle the stationary limit horizon.
To an outside observer looking at this really bright object, the whole thing will appear flattened. So there you have it. A flat black hole...sans all the explanation of the physics. But wait, I haven't finished tormenting your brain yet!
Here's the cool part. If you could travel FASTER than the speed of light, you could theoretically enter the ergosphere (the space between the stationary limit and the event horizon of a spinning black hole) in a Kerr black hole and according to some theories, you could venture along a path which would allow you to avoid colliding with the singularity at the center, and potentially emerge somewhere else, like another universe, or at a time millions or billions of years in the future. If you want to get really funky, you could theoretically position yourself such that you can achieve time travel, owing to the strange effects of the spacetime warp around the event horizon of a black hole! Neat, huh?
Now...before you go sending me emails about how crappy this post was, bear in mind that it's nearly midnight (again) and I'm too tired to be buggered to go make sure my line is straight through this rant. Now go away, before I explain how you don't have any mass! Good night!
I like to consider myself an avid science fiction fan, modest creative-thinker, and to a mediocre degree, author. For this, I find myself highly qualified.
1. I have a degree in Astronomy.
2. I've spent more time in an observatory than I'd like to admit. (Sometimes actually observing...)
3. I've had night-long discussions with fellow astronomers and egg-heads about theoretical physics...
4. I've seen Star-Wars.
Okay, so what about the oranges?
Well I was cooking my dinner tonight, which consisted of a delicately simmered duet of chicken breasts, smothered in a special blend of soft spices, with some lemon, and a bit of orange. While I was peeling said orange, I was reminded of a lecture I attended about a year ago from a leading astronomer who was studying the shape of black holes.
Curiously, black holes aren't always round. Didn't know that? Keep reading, it gets better...
Turns out there are basically two kinds of black holes (that we know of). The kind that spin, and the kind that don't.
As we know from physics, things that spin tend to get flatter. The Earth is a good example, as is the Sun. So is clay on a potter's wheel if the potter walks off to discuss quantum singularities while the motor's still running...which I hear they do a lot...
Anywho, back to the black holes.
A scientist by the name of Karl Schwarzschild spent some time in 1916 playing around with Einstein's field theory equations and came up with a little thing we astronomers like to call the "Schwarzschild Radius." Basically this is the distance from a massive object at which any mass cannot avoid collapsing to a gravitational singularity. In plain-speak, it's the point at which an object's own atomic forces cannot keep the object from shrinking any smaller. Our own Sun is kept from imploding under its massive gravitational force, by the outward force of the fusion reactions inside it. If it weren't for this outward force, the Sun would keep crushing itself smaller and smaller until it became what we astronomers call a "singularity" which is a fancy name for a zero-volume thingy where all the mass went.
So if you had a really massive object...like, hmm...a black hole...the forces causing mass to collapse in would be so great that there would be a point at which any mass would collapse towards that massive object. This is the Schwarzschild radius.
Still with me? Great!
Okay, so we know black holes suck things into them. That's not correct phrasing, but pthtptpt!
We call black holes that don't spin "Schwarzschild Black Holes," because they need a name and "Schwarzschild" is cool-sounding. :)
Actually, they're called that because there is a clearly defined point or radius at which matter traveling towards the gravitational center of the black hole both cannot escape, and cannot avoid being crushed into the singularity, despite its own atoms protests. Schwarzschild black holes are great to work with, because they are nice and docile and don't do anything fancy that messes with normal equations...like spin.
Unfortunately, it is theorized that most black holes spin. We believe this because black holes are formed from massive objects, called stars, which were once spinning. It's very hard to stop an object as massive as a star from spinning. You either need another equal-mass star...or a lot of tiny objects...like...trillions upon trillions upon trillions upon trillions of them... That's another physics issue to talk about later, though.
Okay, so we call rotating (spinning) black holes "Kerr Black Holes" after another famous (well, not so famous) scientist, named Roy Kerr, a New Zealander who got this particular bit of fame in 1963.
Roy Kerr is famous for developing some math equations, known as "Kerr metric," that described the geometry of spacetime around a massive object, such as a black hole. The math will kill brain cells and drive you insane, but from the fingerpaint perspective it's cool stuff.
Get to the point.
Okay, so the point I'm getting at while peeling my orange is that black holes actually deform as they spin. Why is this significant? Well, we all consider black holes to be...well...holes... In a Schwarzschild black hole, that's a pretty good lay-speak way of explaining things. However, in a Kerr black hole, you have a ring. (Trust me, this is a lot more fun when beer is involved...)
Okay, so why a ring now? Well, a funny thing happens when a black hole spins. You see, there's this thing call the "event horizon" which is a catchy term for a spherical boundary at which matter and light can no longer escape the gravitational pull of the black hole singularity. This has been popularized over the years by countless science fiction films, and is probably the part about black holes people know best, and actually get correct. Again, there IS NO HOLE IN A BLACK HOLE!!!
When a black hole spins, it develops two event horizons, actually. One is known as the event horizon, and the other is something we call the "Stationary Limit." The stationary limit is another spherical boundary that defines where an object can not only avoid dropping into the black hole, but remain stationary. You have to be going at the speed of light to make this happen, but we won't split hairs. The key here is that in a Schwarzschild black hole the two horizons are one in the same, while in a Kerr black hole they diverge. The Stationary Limit actually bows out at the equatorial point of the spinning black hole, while at the same time touching the poles of the event horizon sphere. It kinda looks like this, if you could draw it:

Wait, Shoobie...What happened to the ring?
Turns out that a spinning black hole's singularity becomes stretched around it's angular axis (the point in the center) and forms into a ring singularity. This is where the hard-wood physics in most people's brains breaks down and they either get really violent, or start drooling. Just don't send me any hate mail, okay?
What does this have to do with shape, Shoobie? This was supposed to be about the shape of the black hole!
Okay, so you may not be able to see an event horizon, or a stationary limit...but you CAN see the effects of it. According to the laws of particle physics, both horizons will have a photon sphere. A photon sphere is a spherical plane where photons gather, either because they're orbiting, stationary, or just entering the black hole. To tick your brain, photons that enter the black hole traveling WITH its spin (that is, traveling in the same direction as all the stuff the black hole is dragging around it), the photon will nest itself in the inner photon sphere, at the event horizon. If it's going the other way, it will circle the stationary limit horizon.
To an outside observer looking at this really bright object, the whole thing will appear flattened. So there you have it. A flat black hole...sans all the explanation of the physics. But wait, I haven't finished tormenting your brain yet!
Here's the cool part. If you could travel FASTER than the speed of light, you could theoretically enter the ergosphere (the space between the stationary limit and the event horizon of a spinning black hole) in a Kerr black hole and according to some theories, you could venture along a path which would allow you to avoid colliding with the singularity at the center, and potentially emerge somewhere else, like another universe, or at a time millions or billions of years in the future. If you want to get really funky, you could theoretically position yourself such that you can achieve time travel, owing to the strange effects of the spacetime warp around the event horizon of a black hole! Neat, huh?
Now...before you go sending me emails about how crappy this post was, bear in mind that it's nearly midnight (again) and I'm too tired to be buggered to go make sure my line is straight through this rant. Now go away, before I explain how you don't have any mass! Good night!

No comments:
Post a Comment